Properties of a uniformly expanding universe
Observations of distant galaxies suggest that the universe is expanding, but it is not clear exactly how fast and we don’t know the way it is expanding. We have lots of data, but things in the universe are also wandering all over the place and we can only see a part of it. This little discussion is not an attempt to figure out the shape of an expanding universe. What I am attempting here is to just describe a certain kind of simple mathematical model and show what the properties of the model might imply. I thought this model up around 1971 on a family trip to the beach and I’ve been wondering ever since if it has any validity. I doubt if I am the first to consider how inertial frames and an expanding universe are related.
A simple model of the expanding universe.
I want to start with just a map of the velocity associated with points in an expanding universe. This is very linear and non-relativistic and the purpose is just to have a neat, easy to understand way of doing the math. The image below shows the velocity vectors in an expanding universe. There is a center that is at rest and then a certain distance away in any direction things are moving out and the further out you go out, the faster things are moving away from the center.
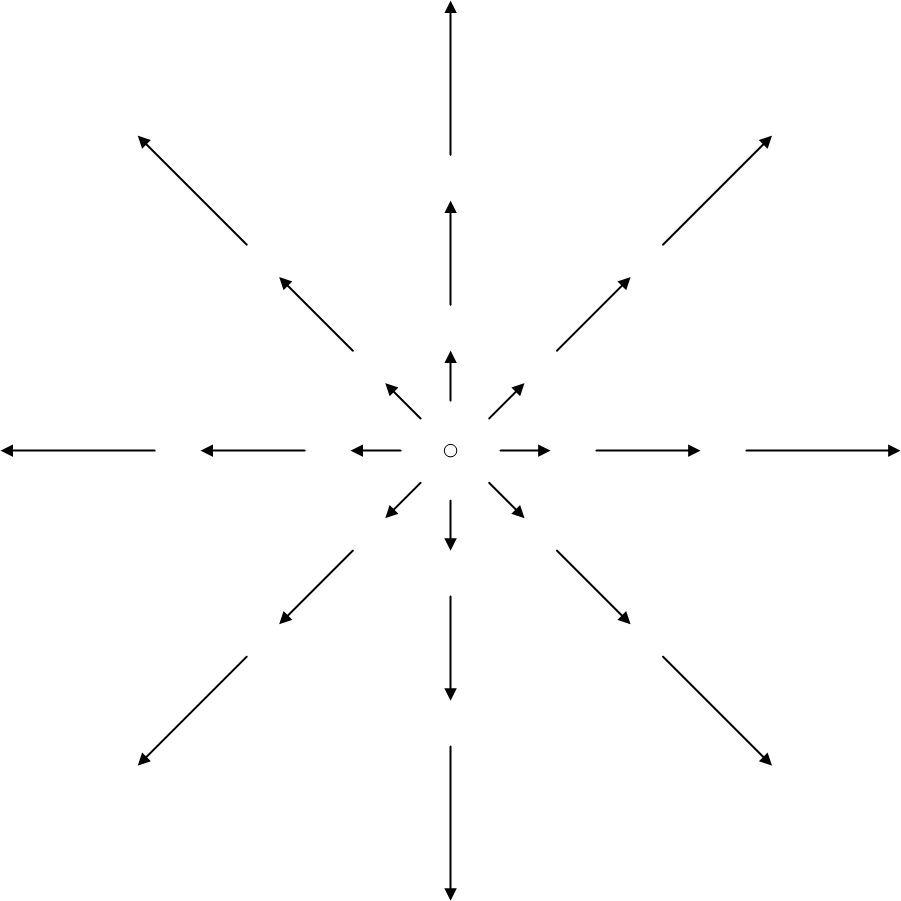
The word center jumps out at you as being very wrong immediately. This model, on the surface seems to imply that there is a point, somewhere in space, that is the absolute center of the universe, but this is misleading and not true.
If you travel, on the diagram above, to the second vector on the right, you will be in an area of space moving away from the center of the universe. If you speed up so that you are “going with the flow” and match the velocity of things in that part of space, you will seem to be holding still in regards to that part of space. If you look back at what used to be the center of the universe, it will be moving away from you. If you look around, the universe is universally expanding way from you just as it had been when you were in the center of the universe. Any measurements that you make of distant stars at this new location indicate that you are at the center of the universe.
Inertial Frames and the Center of the Universe.
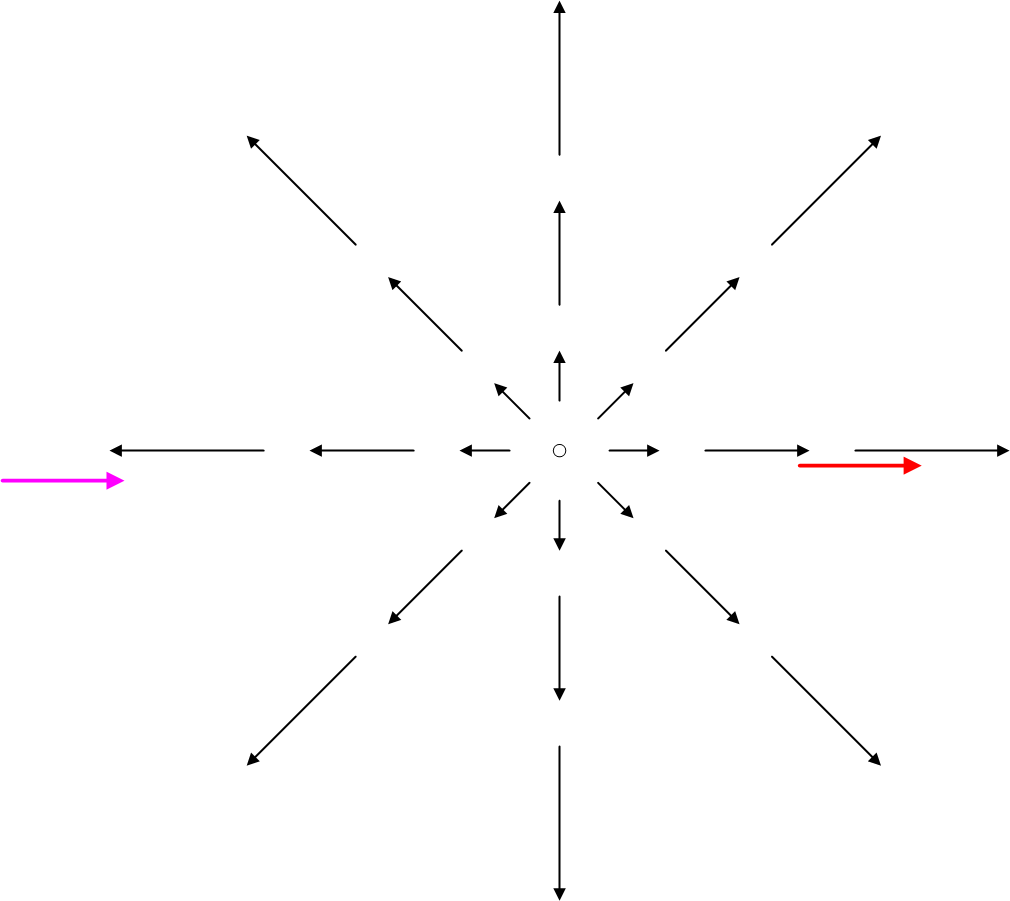
We can easily intuit that for every inertial frame there is a center of the universe. If you are in the center of the universe, you can measure the motion of the distant stars and prove that you are at the center of the universe, at least in this simple model. If you speed up, suddenly the zero center of the universe that matches your inertial frame will be somewhere in front of you.
In the drawing below, the magenta vector on the left represents a person in a spaceship zipping along at a good clip. The red vector on the right hand side is the location in space that matches his velocity, but where the local inhabitants can measure that they are holding still in the center of the universe.
Hubble expansion.
If we use a very simple linear expansion, the velocity at any point it space is a number, called h, times the distance. The units of the Hubble constant is “per second”. Multiply the distance, let’s say 100 meters, times h and we will get the expansion at that point. The expansion 100 meters away is so small as to not be measurable and the Hubble constant is very tiny.
Because in our real world there is a relativistic effect on the distant galaxies, the Hubble constant cannot be linear, but for this simple model we will treat it like it is. Measurements of h are difficult because of the difficulty of observing the far galaxies and estimating their distance, but the current estimates are around 70 km/sec/mpc. This is an odd mixture of units. Convenience in astronomical measurements make an odd mixture of units. MPC is a mega-parsec. Parsec is unit of distance used in astronomy along with light-years and plain old meters.
A mega-parsec is 3.086×1016 m. So the h in meters and seconds is 2.27×10-12 m/s.
H=2.27×10-12 per second
The gravitational effects of a moving body.
The whole reason for considering this model of the expanding universe is to make the claim that there is a gravitational effect on moving bodies. The center of the universe is somewhere in front of a moving body, due to the translation of its inertial frame. The distance to the center of the universe is v/h. The velocity of a moving body, divided by h will give the distance to the center of the universe. The direction, of course, is straight ahead.
Being offset in the universe, the body feels a tug towards the center. You might think that it would be easy to integrate the gravitational forces over the whole universe from minus to plus infinity, but integrating infinities here didn’t work for me.
If you consider a spherical volume of space, centered on the center of the universe, whose radius is v/h where v is the velocity of the body, you can then ignore the universe outside the sphere. The universe outside of the sphere cancels itself out and only the mass inside the sphere counts.
The mass inside the sphere where d is the average density of the universe and r is v/h is pi*d*r3
The force on the moving body (m) is (from the mass center of the sphere):
F=g*m*pi*d*r3/r2
So acceleration=g*pi*d*v/h
The average density of the universe is even harder to estimate than the Hubble constant. There is a consensus that the density is around 5*10-27 kg/m-3
Gravity g is 6.673 × 10-11 m3/kgs2
Multiply it all out and the resulting acceleration of a moving body then is about v x 4.6 x10-25 m/s/s. Call this constant k so acceleration is k*v.
K=4.6 x10-25 /s
Let’s figure what the effect might be on a probe like pioneer or voyager that is moving outbound at around 1.5 x104 m/s.
The acceleration would be 6.9 x10-21
If you figure that a probe has been travelling 1000 days or 86,400,000 seconds, and simply multiplying the time times the acceleration then the increase in speed is on the order of 10-13 meters/second.
The aberrations reported on at least some of the probes are 1.3*10 -3 m/s, which is a little high for this effect.
However, I used the average density of the universe. The local area space is a little denser. The size of the sphere we are talking about is v/h or about 6.6 * 1015 which is less than a light year. There is a lot of stuff within a light year of earth.
If I use a higher value for the density then things go way up. Since I have no idea what value to use as the density of the local universe and the mass is not symmetrical, all I can say us that the inertial frame may have a measurable effect on the movement of a space probe, but I can’t really say more.
What I can say is that a fast moving particle that left a star about 2 billion years ago and has travelled through empty space the whole way will pick up a more than a little speed during its travels and it might explain cosmic rays.
Why doesn’t this violate conservation of energy and mass? All I can say is that perhaps the law is more of a suggestion than a law. If you look at the expanding universe being in a nice steadily expanding state with all bodies knowing their own inertial state then there is no problem, but the body’s equilibrium can be tipped by pushing a little on it and then rolls down hill until it hits someone hard as a cosmic ray a billion years later.
I wonder what the potential energy is for a body in equilibrium in the expanding universe. If you tip it, will its total eventual kinetic energy be M C squared? If this is true, might there be a relationship between, the Hubble constant, the mass of the universe and the speed of light implied in the above calculations?
Naturally, the Hubble acceleration isn’t linear when you start getting edging up closer to C. A nice model would take the contraction of space and the mass increase on moving bodies as the inertial center of the universe changed for very fast moving objects. I would guess that the density of the enclosing sphere would go up as the velocity of a particle goes up. The shape of the sphere might distort, also the center of the universe will be adjusted. The basic idea would remain the same. This would still explain cosmic radiation well.
Practically, we seem to be getting energy out of a moving body. Would it be possible to get a particle moving to the point where we could bleed off the extra acceleration as usable energy? Would the next power plant be a neat little cyclotron zipping electrons around a track and capturing those that increased in speed as an infinitely renewable power source?
The speed of light is about 3×108 m/s so if we could get an electron up to about 108 m/s then the acceleration would be about 5×10-17. We’d have to have quite a few electrons moving. The mass of electron is about 10-32 kg so the force on the electrons would be damn tiny, about 5×10-49 joules. A coulomb is about 6×10-18 electrons, so a coulomb yields about 10-31 volts. Unless you could accelerate the electrons up to near the speed of light then there won’t be any cheap sources of energy from this.
5 Comments
-
-
Keith says:
“Why not asymmetric expansion?”
If permit my comentary:
It’s against Hubble’s law.
In my web I affirm that “Expansion only can be constant” in proof 5p.
The relation between years we see and years from begin of universe only admit that expansion is a light speed.
-
There is the Hubble’s law – http://en.wikipedia.org/wiki/Hubble%27s_law
“There are some observations that not everything seems to follow Hubble in a consistent manner. The expansion factor seems to vary as to which way you look and what you look at.” – if I don’t remember bad is “recessional velocity” also in the same article. (it’s in the same article but I don’t remember if this is what you say)
I’m against Universe expansion:
In my blog I say that only can expand in spherical mode how I say in your images.
For example a question: – The universe expand in any radius at light speed: How can accelerate? At what speed expand the diameter (radius x 2)?
This and more, also doubts, proofs and hypothesis in http://bigbangno.wordpress.com
Thanks.